데이터 통신

[Data Communication] 아날로그 신호 -> 디지털 데이터로의 변환

짱일모 2023. 3. 14. 17:46

물리 계층에서 신호의 모양

물리계층에서는 신호는 0 / 1 즉, 비트로 이루어져 있습니다.

 

아날로그 신호의 모양

아날로그 신호는 사인함수의 조합으로 구성되어 있습니다.

 

sin 함수

특히 소리의 경우 높낮이가 주파수, 크기가 Amplitude 로 표현된다는 것을 과학시간에 배운적 있으실겁니다. 인위적으로 진동수와 Amplitude 를 고정한 채 261.626Hz 의 진동을 발생시킨다면 흔히 아는 "도(C)" 의 음높이를 갖는 소리를 들을 수 있을겁니다.

 

하지만 피아노, 기타와 같은 악기로 같은 "도(C)" 음을 발생시켰을 때 우리는 이것이 도의 음높이를 가진다는 것도 알 수 있지만 이 소리가 기타의 소리인지 피아노의 소리인지도 구분할 수 있습니다. 이것이 가능한 이유는 기타가 발생시키는 파형과 피아노가 발생시키는 파형이 서로 다르기 때문입니다.

 

아날로그 신호는 사인함수의 조합으로 이루어진다고 했습니다. 소리는 아날로그 함수이므로 소리 또한 여러 사인함수의 조합으로 표현될 수 있습니다. 앞서 예시를 들은 피아노 소리와 기타소리도 마찬가지입니다. 피아노 소리, 기타 소리도 서로 다른 진동수와 진폭을 갖는 여러 사인함수들의 조합으로 이루어집니다.

 

다음은 피아노 소리와 기타 소리를 주파수와 진폭을 축으로 하여 나타낸 그림입니다.

여러 주파수와 진폭들로 이루어진 소리의 조합이 실제 아날로그 신호!, http://physicstutor.kr/1772

만약 아까 예시로 들은 인위적인 진동수와 진폭을 갖는 소리를 진동수 - 진폭을 축으로 하여 그림을 그린다면 하나의 막대만이 나타날 것입니다.

 

"소리" 를 구체적으로 예시를 들어 설명했지만 앞선 설명은 비단 소리에만 국한되는 것이 아닌 "아날로그 신호" 전체에 적용됩니다.

 

그렇다면 

 

사인 함수 형태의 아날로그 신호를 어떻게 디지털 신호로 변환할 수 있을까요?

 

먼저, 디지털 신호 0 / 1 즉, 비트도 다음과 같이 사인함수의 형태로 나타낼 수 있다는 것을 알아둡시다.

올라가 있으면 1, 내려가 있으면 0 => 양의 전압은 1, 음의 전압은 0

 

아날로그 신호의 디지털 신호로의 변환 과정 (표본화 - 양자화 - 부호화)

어떤 소리(아날로그 신호)가 아래 (a) 와 같은 형태로 들어왔다 생각합시다.

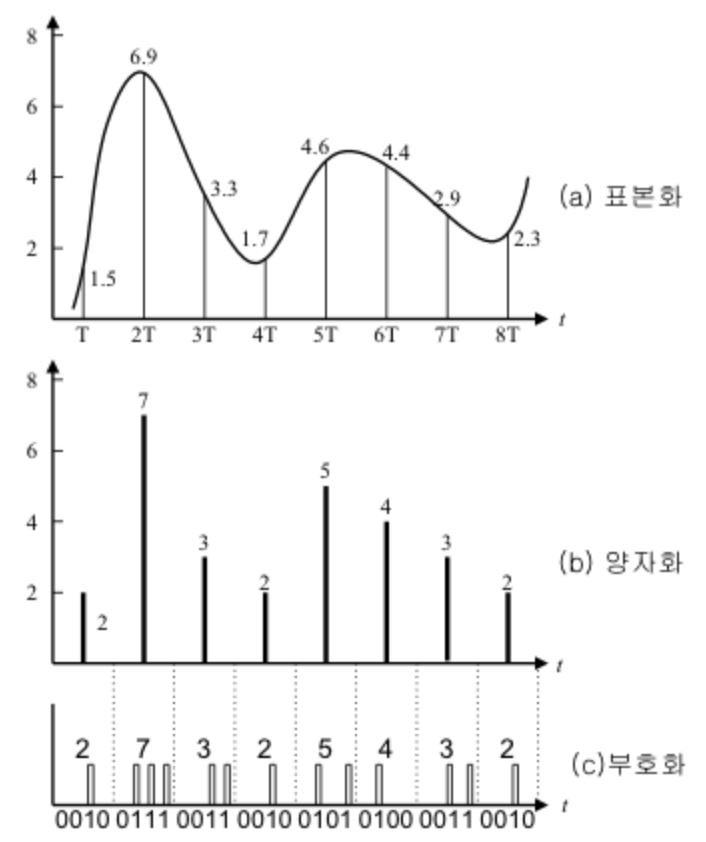
https://velog.io/@devmoonsh/Computer-Science-아날로그-소리를-디지털로-변환하는-법

 

그리고 소리의 특징이 되는 값을 나타낸 뒤 이것을 양자화 하고, 부호화하여 0, 1 즉 비트로 전송할 수 있는 형태로 만듭니다.

 

이 경우 sampling rate 는 1/T, bit per sample 은 4입니다. 즉, 한 순간(sample) 에 이 데이터가 가질 수 있는 소리의 형태는 16가지입니다. sampling rate 가 작을 경우, 손실되는 소리가 생길 것입니다. 이 16가지의 신호는 5V 전압을 이용해 표현한다면 0000 ~ 1111 을 5V / 2^4 * (0000 ~ 1111) 로 표현할 수 있을 것입니다. 

 

다음 그림을 보며 wav 파일의 구조와 sampling rate, bit per sample, bit per sec 에 대해 알아봅시다.

 

wav structure, sample rate

위 사진의 경우, 1초에 10개의 sample 을 만들었습니다. 즉, sampling rate 는 10Hz 입니다. 그리고 1개의 샘플에 스테레오 즉, LEFT, RIGHT 데이터가 존재하므로 한 개의 sample 에 16개의 bits 가 들어있습니다. 따라서 이 샘플이 가질 수 있는 소리의 형태는 2^16 개입니다. 그리고, sampling rate (sample number / sec) 와 한 샘플 당 비트 수( bits / sample number) 의 곱인 (bit / sec) 에 의해 이 아날로그 신호의 1초동안의 데이터는 sampling rate * bit per sample 만큼의 비트수로 저장이 됩니다.

 

그렇다면 어느정도의 Sampling Rate 가 적당할까요?

Nyquist Sampling Theorem 에 따르면 Perfect 한 Reconstruction 을 위해서는 아날로그 신호에서 fastest 한 주파수의 적어도 2배의 frequency 로 Sampling 해야 한다고 합니다. 즉, Nyquist Theorem 에 따르면 샘플링 레이트 * 0.5 보다 빠른 주파수를 가진 고음 영역은 손실이 더 커집니다. 그래서 Sampling Rate * 0.5 = Nyquist Limit 이라 부릅니다.

 

따라서 원본에 가까운 아날로그 신호를 저장하는 것을 결정짓는 요소 (Determinant) 는 ...

  • Sampling Rate (1초의 아날로그 신호를 얼마나 샘플링 할 것인가, Sampling 단계, Nyquist Theroem)
  • Bit Per Sample (한 샘플을 얼마의 비트 개수로 표현할 것인가?, Quantizing 단계)
  • 채널의 개수

사람의 목소리를 잘 저장하려면 1초에 몇 비트가 처리되어야 할까요?

-> 2 channels * 4000Hz Sampling Rate (Nyquist Limit 2000 * 2, Sample per sec) * 8bits (Bits per Sample) = 64000bits per sec 

 

예시로, python 의 pyaudio 를 사용하여 소리를 녹음하는 것에 대해 살펴봅시다.

위 코드를 살펴보면, WAV 파일 생성시 필요한 environment 설정이 되어있습니다.  각 변수의 역할은 다음과 같습니다.

  • FORMAT = pyaudio.paInt16: 오디오 샘플링 데이터의 형식을 지정하는 변수입니다. pyaudio.paInt16은 16비트 정수형 형식으로, 오디오 데이터가 16비트로 표현되어 있다는 것을 의미합니다.
  • CHANNELS = 2: 녹음할 오디오 데이터의 채널 수를 지정하는 변수입니다. 이 코드에서는 스테레오 녹음을 수행하기 위해 채널 수를 2로 지정하였습니다.
  • RATE = 44100: 오디오 샘플링 레이트를 지정하는 변수입니다. 이 코드에서는 44100Hz로 샘플링 레이트를 지정하였습니다. 이는 CD 품질의 오디오를 표현하기 위한 일반적인 샘플링 레이트입니다.
  • CHUNK = 1024: 오디오 데이터를 처리하는 단위 크기를 지정하는 변수입니다. 이 코드에서는 1024개의 샘플링 데이터를 처리하는 단위로 지정하였습니다.
  • RECORD_SECONDS = 6: 녹음할 시간을 지정하는 변수입니다. 이 코드에서는 6초 동안 녹음을 수행합니다.
  • WAVE_OUTPUT_FILENAME = "test.wav": 녹음한 오디오 데이터를 저장할 파일 이름을 지정하는 변수입니다. 이 코드에서는 "test.wav"라는 파일 이름으로 저장합니다. 이 파일은 WAV 형식으로 저장되며, FORMAT, CHANNELS, RATE 등의 정보를 포함합니다.

그리고 두번째 칸의 코드에서 for loop 을 RATE / CHUNK * RECORD_SECONDS 만큼 반복합니다. 이는 6초 동안의 총 CHUNK 수와 일치하며 위 설정값을 바탕으로 이것은 258 로 계산됩니다. 즉 6초 동안 258개의 CHUNK 가 저장됩니다.

 

그리고 세번째 칸의 코드에서 녹음된 frames 를 바탕으로 wav 파일을 생성합니다.

 

이렇게 앞에서 설명한 것처럼 아날로그 신호가 디지털 신호로 변환되어 전송될 수 있습니다.