[Algorithm] 방해꾼 논법 (Adversary Argument)
어떤 문제를 해결하는 데 걸리는 소요시간의 lower bound 를 찾는 방법 중의 하나인 방해꾼 논법에 대해 알아보겠습니다.
방해꾼 논법 (Adversary Argument)
1. 해결하는 사람 (Solver) 와 상대방 (Adversary) 간의 일종의 스무고개 같은 게임입니다.
2. Adversary 는 input 을 가지고 있고, solver 는 input 이 무엇인지 확인할 수 없습니다.
3. solver는 adversary 에게 질문을 할 수 있습니다. 이 때, 질문은 형식에 맞춰 질문해야 합니다. ( 알고리즘의 계산 모델 제약 조건이 질문의 형식 제약이라고 생각할 수 있습니다. )
4. adversary는 solver 의 질문에 대해 답변을 해주어야 합니다. 이 때, solver 가 최대한 늦게 문제를 해결하도록 input 을 계속 바꿀 수 있습니다.
5. 단, input 을 바꿀 때 일관성(consistently)를 유지해야 합니다. 즉 이미 대답해준 결과에 위배되도록 input 을 바꿀 수는 없습니다.
6. 이 과정을 통해 Algorithm 의 lower bound 는 solver 에게 필요한 최소한의 질문 횟수가 됩니다.
Array A[1,2,3,4,5] 에서 maximum element 의 위치를 찾는 문제를 해결하는 알고리즘의 lower bound 를 방해꾼 논법을 사용하여 증명해보도록 하겠습니다. 이 때, Array의 각 Element는 모두 다르다 가정하겠습니다.
앞서 말씀드린 solver 가 adversary 에게 질문할 때 질문의 형식이 되는 제약 조건은 오직 'A의 i번째 element는 j번째 element보다 큰가?' ( A[i] > A[j] 인가? ) 만 허용된다는 것입니다.
먼저 Upper Bound 에 대해 알아봅시다. 5개의 서로 다른 숫자가 있을 때 가장 큰 수를 찾는 간단한 방법은 4번의 비교 수행하는 것입니다. (Max = A[1] 로 두고, max(Max, A[2]), max(Max, A[3]) ... max(Max, A[5]) 를 수행)
Bob과 Elice의 문답을 통해 방해꾼 논법 (Adversary Argument)에 대해 이해해봅시다.
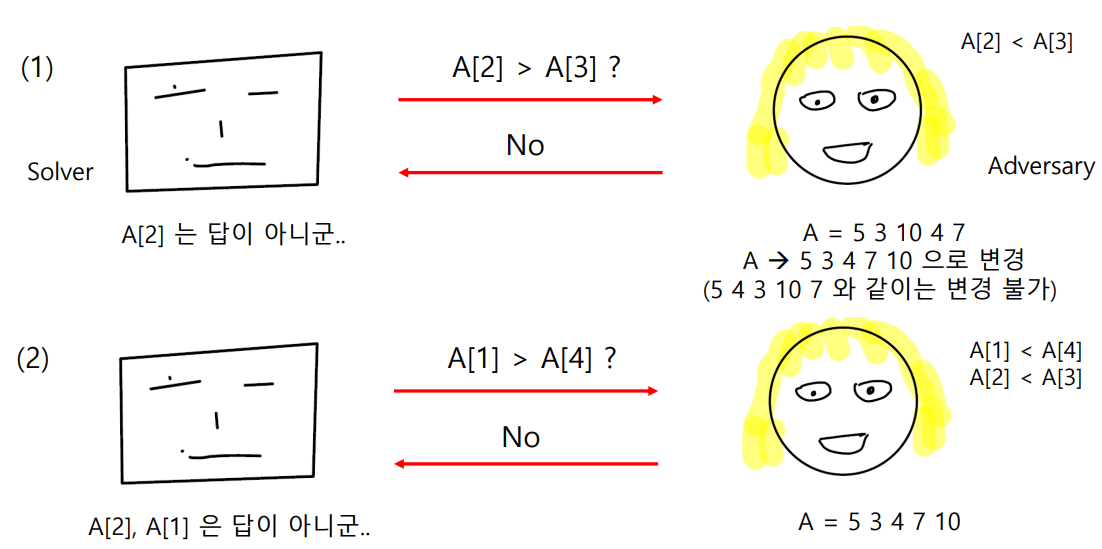
먼저, Adversary 는 input 으로 A = [5,3,10,4,7] 을 갖고 있습니다.
첫번째로 Solver 는 A의 2번째 원소가 3번째 원소보다 크냐고 묻습니다. Adversay 는 No 라고 답하고 input 을 A = [5,3,4,7,10] 으로 변경합니다. Adversary 는 input A를 A[2] < A[3] 을 만족하는 어떤 배열로든 바꿀 수 있습니다.
( 추가적으로 첫번째 질문 시에는 Adversary는 input 이 충족해야할 어떤 규칙도 가질필요가 없으므로 Adversary 가 [ 5,10,3,4,7] 을 가지고 있을 때 solver 가 'A[2] > A[3] ?' 의 질문을 하더라도 YES 라고 답할 필요가 없습니다. NO 라고 답하고 input 을 A[2] < A[3] 을 만족하는 아무 배열로 바꿔버리면 그만이기 때문입니다. )
두번째로 Solver 는 A의 1번째 원소가 4번째 원소보다 크냐고 묻습니다. Adversary 는 No 라고 대답합니다. Adversary는 input A 를 A[1] < A[4], A[2] < A[3] 을 만족하는 어떤 배열로든 바꿀 수 있습니다.
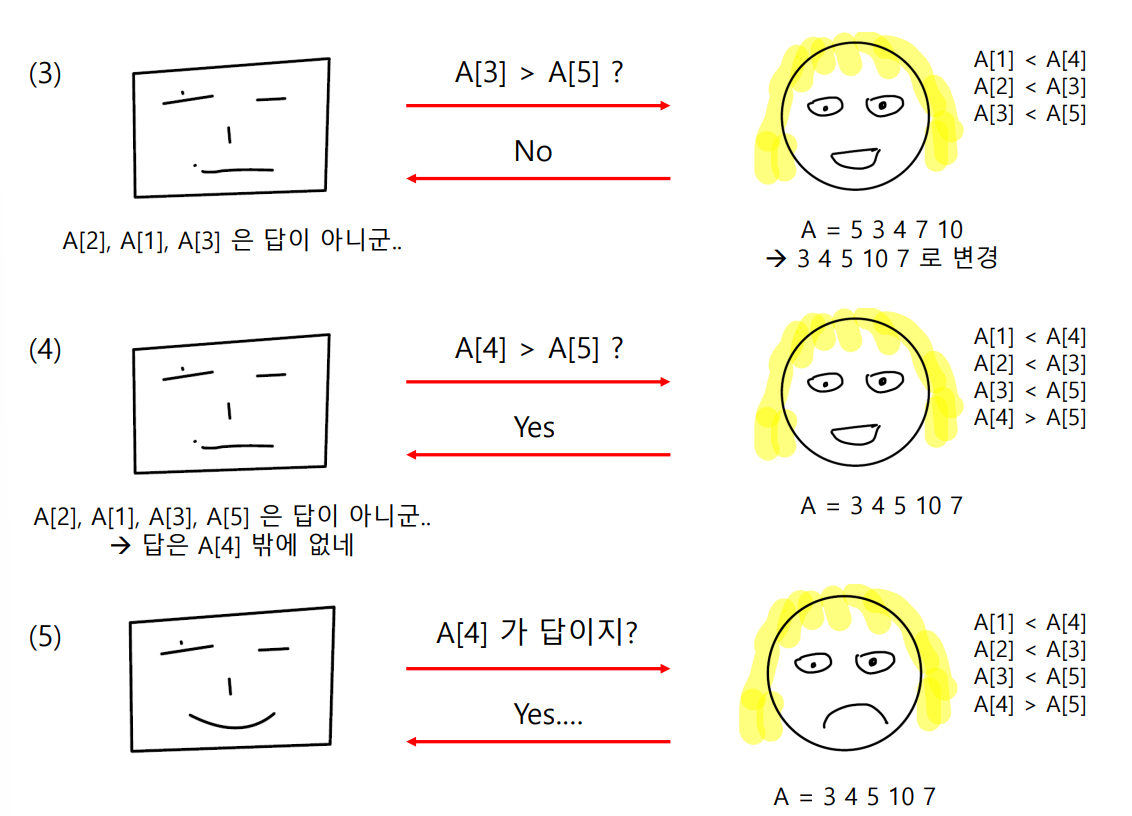
세번째로 Solver 는 A의 3번째 원소가 5번째 원소보다 크냐고 물어봅니다. Adversary는 No 라고 답하고 input 을 A = [3,4,5,10,7] 로 변경합니다. Adversary 는 input을 A[1] < A[4], A[2] < A[3], A[3] < A[5] 를 만족하는 어떤 배열든 바꿀 수 있습니다.
네번째로 Solver 는 A의 4번째 원소가 5번째 원소보다 크냐고 묻습니다. Adversary 는 YES 라고 답합니다. 이 때, Solver는 그 동안 질문한 내용을 바탕으로 2,1,3,5 index는 maximum element가 될 수 없음을 알고있습니다. 배열의 원소는 총 5개이므로, 아직 물어보지 않은 4가 maximum element 임을 확정할 수 있습니다.
지금까지 살펴본 방해꾼 논법을 바탕으로 위 문제의 Lower Bound 를 증명해보겠습니다.
Directed Graph G = (V, E) 를 다음과 같이 정의합시다.
- V = { 1, 2, 3, 4, 5 }
- E : Solver가 A[i] > A[j] 라는 대답을 Adversary에게 받을 때마다 edge(j,i) 를 추가합니다. (Topology Order를 떠올려봅시다.) 따라서 G의 edge 개수는 현재까지 주고받은 질문 개수임과 동시에 수행한 비교 횟수가 됩니다.

Solver 가 답을 확정할 수 있기 위해서는 최소 4개의 Edge 가 필요합니다. 따라서 이 문제의 lower bound 는 4가 됩니다.
4번보다 적게 비교 시 (위의 그림에서는 3번을 비교했습니다.) 최소 두개의 connected component 가 생성되고 (최소 두개의 sink 가 생성) 서로 다른 두 component 에 속한 두 원소를 adversary 가 마음대로 바꿀 수 있기 때문입니다. 즉 정답을 확정할 수 없게됩니다. 같은 방법으로 size n 인 array 의 경우 n-1 lower bound 를 증명할 수 있습니다.
이번에는 방해군 논법을 이용하되, 다른 방법으로 위 문제를 해결하는 알고리즘의 lower bound 를 증명해보도록 하겠습니다.
Adversary 와의 문답에 의해 A[j] > A[i] 임이 판명난 경우 j 는 i 에 이겼다고 이야기합시다. (혹은 i 는 j 에게 졌다고 이야기합시다.) 이것을 가지고 Array 의 index 들을 다음과 같이 세 집합으로 나누어봅시다.
- W (Win) : 한 번 이상 이겼으면서 한 번도 지지 않은 index 들의 집합
- L (Lose) : 한 번 이상 진 index 들의 집합
- N (Not yet) : 한 번도 비교하지 않은 index 들의 집합
Adversary 와 문답을 주고 받기 전 초기 상태는 W 과 L 은 공집합, N = {1,2,3,4,5} 가 됩니다.
N = 공집합, L 의 size 가 n-1 이면 W 에 있는 index 가 maximum element의 index 가 됩니다.
index 가 다른 집합으로 옮겨갈 때 credit 을 얻을 수 있다고 해봅시다. credit 의 획득은 다음과 같이 정의해봅시다.
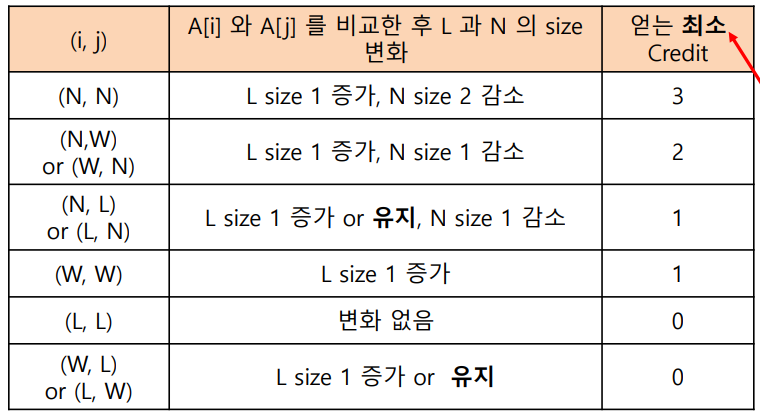
Case 가 많아보이지만 실상은 간단합니다. 집합 N 의 사이즈가 1 감소하거나, 집합 L 의 사이즈가 1 증가하는 경우, credit 1을 획득합니다. Credit 을 최소 Credit 으로 설정한 이유는 최악의 경우를 고려하기 위함입니다.
이 문제를 해결하기 위해서는 최소 9의 크레딧이 필요함을 직관적으로 알 수 있습니다. 다음 그림을 통해 살펴봅시다.
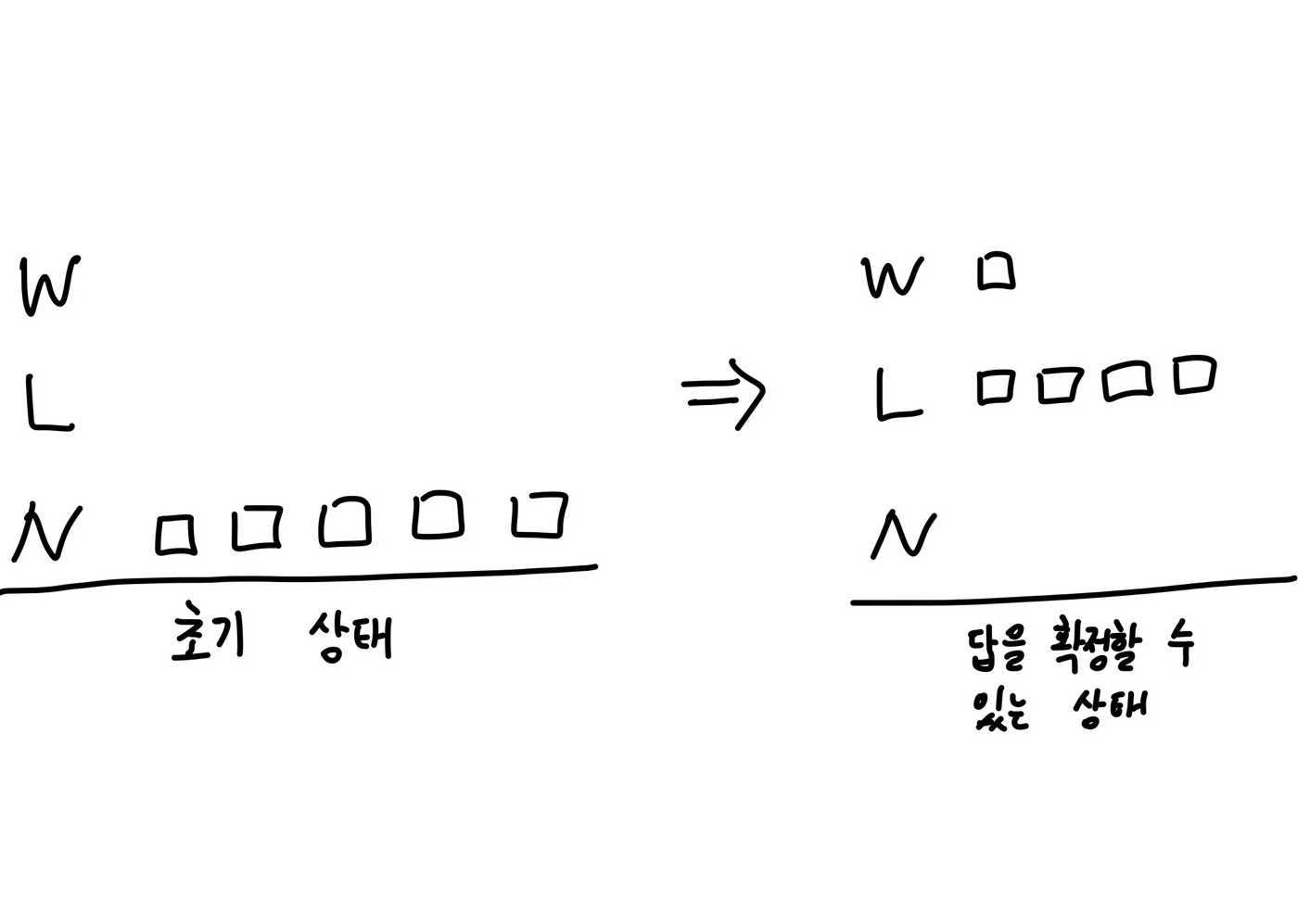
Solver 는 Adversary 와의 문답을 통해 W, L, N 을 계속 Update 해줄 수 있습니다. (A[i] > A[j] 를 계속해서 물어보기 때문입니다!)
그렇다면 9 크레딧을 벌면, 답을 확정할 수 있는 상태가 됨을 알았습니다. 어떻게 해야 최소의 질문으로 9 크레딧을 벌 수 있을까요? 다시 한번 아까 보았던 Credit Table을 봅시다.

먼저 가장 많은 크레딧을 얻을 수 있는 행동은 집합 N 에 속한 두 인덱스를 비교하는 질문을 Adversary 에게 던지는 것입니다. 우리의 문제에서는 총 원소의 개수가 5 이므로, (N, N) 질문을 최대 2번 던질 수 있습니다. 따라서 6 Credit 을 획득할 수 있습니다.
그러면 나머지 3점을 채우기 위해서는 어떻게 해야할까요? 3점을 채우기 위해선 이제 적어도 2개의 질문을 던져야 합니다. 1회 질문으로 얻을 수 있는 최대 Credit 이 2 이기 때문입니다. 따라서 적어도 4번의 질문을 던져야 함을 알 수 있습니다.
따라서 이 문제를 해결하는 알고리즘의 lower bound 는 4라고 이야기 할 수 있습니다.
되짚어보면, Lower Bound 를 증명하기 위해서 방해꾼 논법을 사용했지만 이 과정에서 구체적인 알고리즘을 사용한 적이 없습니다. 오로지 비교연산을 통해 문제를 해결하기 위해 몇 번의 비교를 해야하는가만 따졌습니다.
즉 Lower Bound 와 문제를 해결하는 특정 알고리즘은 아무런 관계가 없습니다.