[Algorithm] Longest Increasing Subsequence (LIS 문제)
Dynamic Programming 기법으로 해결할 수 있는 대표적인 문제인 LIS (Longest Increasing Subsequence) 문제입니다.
먼저 Subsequence 의 정의부터 알아보겠습니다.
길이 n인 Sequence (ordered list) S = a1, a2, ... , an 이 주어졌을 때, sequence S' = ai1, ai2, ..., aik 가 1 <= i1 < i2 < ... < ik <= n을 만족할 경우 S'을 S의 subsequence 라고 합니다.
*주의 : Subsequence 와 Substring 은 다른 개념입니다.

이번에는 increasing sequence 란 무엇인지 알아보겠습니다.
a1 < a2 < ... < an 일 때, sequence S는 increasing sequence 라 하며, a1 <= a2 <= ... <= an 일 경우 sequence S 는 non-decreasing 이라고 합니다. decreasing 과 non-decreasing 도 부등호의 방향을 바꾸고 strictly less 조건만 잘 구분하며 비슷하게 정의할 수 있습니다.
이제, Longest Increasing Subsequence (이하 LIS) 문제에 대해 정의하겠습니다.
Input : Sequence S = a1, a2, ... , an
Problem : S 에서 제일 긴 increasing subsequence 의 길이 구하기
LIS 의 예시를 하나 살펴보겠습니다.

이전 포스팅에서 이야기했던 Dynamic Programming 기법을 사용하여 문제를 해결하는 절차에 대해 다시 한번 살펴보며 LIS 문제를 해결해 보도록합시다.
Dynamic Programming 으로 문제를 해결하는 절차는 다음과 같습니다.
1. 문제를 정확하게 정의하기. (구하고자 하는 것이 무엇인지 정확하게 파악해야 합니다.)
2. 정의된 문제에 대한 subproblem 을 정의한 뒤 subproblem 을 이용한 recurrence relation 을 세우기. (subproblem 이란 본래 문제보다 size가 작은 문제를 의미합니다. fibonacci 문제에서는 fn' (n' < n) 이 subproblem입니다.)
3. Memoization 을 이용하여 recurrence relation 을 계산
중간 결과물들을 저장할 자료구조 (Data Structure) 를 골라야합니다.보통은 n차원 array 를 사용합니다.
Subproblem 들 간의 dependency 를 확인합니다. ( fibonacci 문제의 Fn을 구하려면 어떤 subproblem 들을 계산해두어야 할까요? 바로 Fn-1과 Fn-2 입니다.)
Dependency 에 기반하여 subproblem 들의 답을 구하는 순서를 정해야합니다. ( fibonacci 문제는 1차원 array 이므로 그냥 순차적으로 구하면 됐습니다.)
4. Time Complexity 분석 및 알고리즘을 작성하기.
앞서 1번을 해결했으니 2번 절차를 밟아보도록 하겠습니다.
Subproblem L[i]를 다음과 같이 정의해봅시다.
L[i] : S의 첫 i개의 element a1, a2, ... , ai 로 이루어진 sequence 에서 LIS 의 길이
위의 경우 L[i]를 L[1], L[2], ... L[i-1]로 나타낼 수 있을까요? 즉 Recurrence Relation 을 세울 수 있을까요?
Case 1) 길이 L[i] 의 increasing subsequence Si 가 ai를 포함하지 않는 경우, L[i] = L[i-1] 이 성립합니다.
Case 2) Si 가 ai 를 포함한다고 하면, Si 에서 ai 바로 직전에 나오는 element 는 aj (j < i and aj < ai) 가 될 것입니다.
이것에 해당하는 j 는 바로 알 수 없으므로 모든 가능성을 생각해보아야 합니다.
따라서, Recurrence Relation 은 다음과 같이 됩니다.
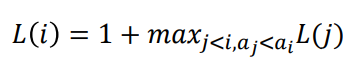
위 Recurrence Relation 은 타당한가요? 그렇지 않습니다. 왜나하면 L[j] 가 aj를 포함하는 지 보장할 수 없기 때문입니다. (앞에서 Si가 ai를 포함할 때 ai 바로 직전의 element 는 aj가 되어야한다고 했는데 L[j] 의 마지막 element가 aj가 아닐 수도 있기 때문입니다.)
즉, 앞서 정의한 Subproblem 은 타당하지 못하므로 Subproblem 을 타당하게 재정의할 필요가 있습니다.
이번에는 올바른 방법으로 Subproblem 을 정의해보도록 하겠습니다.
방금 다루었던 타당하지 못한 Subproblem 에서 발생한 문제는 L[j] (j<i and aj < ai) 가 "element aj를 포함하는지" 를 "보장"하지 않았기 때문에 발생했습니다. 따라서 이번에는 다음과 같이 Subproblem 을 정의하겠습니다.
L[i] : 첫 i개의 element a1, a2, ..., ai 로 이루어진 sequence 에서 ai 로 끝나는 increasing subsequence 중 가장 긴 subsequence 의 길이라고 정의합시다.
L[i] 를 위와 같이 정의한 경우 다음과 같은 recurrence relation 을 만족한다는 것을 알 수 있습니다.
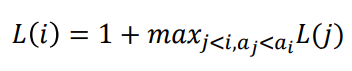
이 경우 S의 LIS 길이는 max(i=1 to i=n)L[i] 가 됩니다.
이제 3번 절차를 밟아보겠습니다.
Data Structure 선정 : L[i] 를 구하기 위해서 L[1] 부터 L[i-1] 까지의 값만 알면 되므로 1차원 Array를 사용하겠습니다.
Subproblem 간의 Depedency 파악 : L[i] 를 구하기 위해서 L[1] 부터 L[i-1] 까지의 값만 알면 됩니다.
답을 구하는 순서 : L[1] 부터 오른쪽으로 순차적으로 해결해나가면 됩니다.
def findLIS(S):
n = len(S)
L = [1] * n
for i in range(n):
for j in range(i):
if (S[j] < S[i]) and ((1+L[j]) > L[i]):
L[i] = 1 + L[j]
return max(L)위 코드는 Array L 에 Subproblem L[i]의 값들을 memoization 해가며 LIS 를 문제를 해결하는 코드입니다.
마지막으로 4번 절차인 Time Complexity 를 계산해보면
1. L[i] 를 계산할 때 조건에 맞는 L[j] 를 탐색 => O(i-1)
2. 1번을 i = 1, 2, ... , n-1 에 대해 수행하므로 O(1+2+3...+n-1) = O(n^2)
3. max(L) 수행 => O(n)
따라서 Dynamic Programming 을 이용하여 LIS 를 해결하는 위 알고리즘은 O(n^2) 의 시간복잡도를 가집니다.